Doğrusal Denklemler Konu Anlatımı

Doğrusal Denklemler Konu Anlatımı: Matematikteki doğrusal denklemlerin çözüm yöntemlerini, uygulamalarını ve bu konseptin günlük hayattaki etkilerini öğrenin.
DOĞRUSAL DENKLEM NEDİR?
Doğrusal ilişkiyi göstermek için kullanılan denklemlere doğrusal denklem denir.
x ve y değişken (bilinmeyen) , a ve b katsayı ve c ise sabit terim olmak üzere: ax + by + c = 0 şeklinde olan denklemlere doğrusal denklem denir.
Bir taksinin taksimetresi açılışta 20 ₺ ve gidilen her kilometrede 10 ₺ yazmaktadır. Şimdi bu ilişkiyi tablo ve grafikle gösterelim.
| Yol (km) | Ücret ( ₺ ) | İlişki |
| 0 | 20 | 20+0×10 |
| 1 | 30 | 20+1×10 |
| 2 | 40 | 20+2×10 |
| 3 | 50 | 20+3×10 |
Tablo ve grafik incelenirse veriler arasında doğrusal bir ilişki olduğu görülür.
Bu ilişkiyi yazacak olursak:
ÜCRET = 20 ₺ + YOL x 10 ₺
ü = 20 + y . 10
x=20+10y (ücret x , yol y olsun)
Bu oluşturduğumuz denklem doğrusal denklemdir.
Burada ücret değişkeni gidilen yola bağlı olduğu için ücret bağımlı, yol bağımsız değişkendir.
DOĞRUSAL İLİŞKİ İÇEREN GRAFİKLERİ YORUMLAMA
Doğrusal ilişki içeren grafikleri yorumlarken aşağıdaki yöntemleri kullanabiliriz.
Doğru üzerinde verilen bir noktanın koordinatlarından yararlanılarak grafik yorumlanabilir.
Örnek:
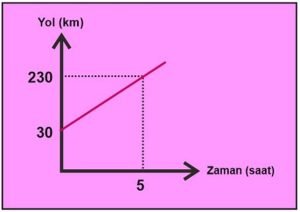
Yukarıda verilen grafik bir aracın Mersin’e olan uzaklığının zaman bağlı değişimini göstermektedir.
Buna göre bu aracın 12. saatin sonunda Mersin’e olan uzaklığı kaç km olur?
Aracın başlangıçta yani hiç hareket etmeden Mersin’e olan uzaklığı 30 km’dir.
Verilen grafiği incelediğimizde araç yolun 30 km’si ile 230 km’sini 5 saatte almıştır. Yani bu araç 200 km yolu 5 saatte almıştır.
5 saatte 200 km yol alırsa 1 saatte 40 km yol alır.
1 saatte 40 km yol alırsa 12 saatte 480 km yol alır.
Başlangıçta 30 km yol aldığı için 480+30=510 km 12 saatin sonunda aracın Mersin’e olan uzaklığıdır.
Örnek:
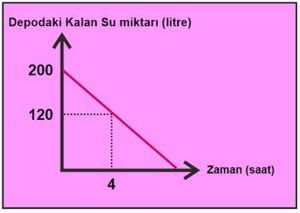
Başlangıçta 200 litre su bulunan bir depodaki su miktarının zamana bağlı değişimi yukarıdaki grafikte verilmiştir.
Buna göre depodaki suyun tamamı kaç saatte tükenir?
Yukarıdaki grafik türü azalan zaman grafiğidir. Yani zamanla depodaki su miktarı azalmaktadır.
Grafiği incelediğimizde depoda başlangıçta 200 litre su vardır.4 saat sonunda 120 litre su kalmıştır. Yani 4 saatte depoda 80 litre su boşalmıştır.
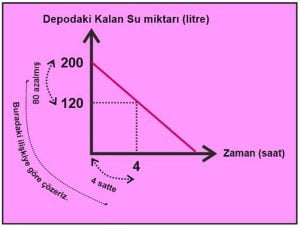
4 saatte 80 litre su akarsa 1 saatte 20 litre su akar.(orantı kurarız)
200 litre su 200÷20=10 saatte su akar.
Verilen doğru grafiğinin doğrusal denklemini oluşturarak grafik yorumlanabilir.
Örnek:
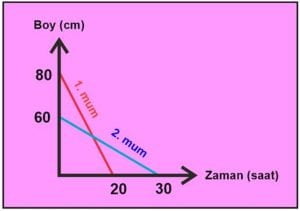
Yukarıdaki grafik iki ayrı mumun zamana bağlı değişimini göstermektedir.
Buna göre ;
- a) Kaç saat sonra mumların boyu eşit olur?
Yukarıdaki grafiği yorumlamak için 1.mum ve 2.muma ait doğrusal denklemini oluşturalım.
1.mumun doğrusal denklemi
Birinci mum 20 saatte 80 cm tükeniyor.
1 saatte 4 cm tükenir.
Birinci mumum doğrusal denklemi = 80-4x
2.mumun doğrusal denklemi
İkinci mum 30 saatte 60 cm tükeniyor.
1 saatte 2 cm tükenir.
İkinci mumum doğrusal denklemi = 60-2x
Birinci ve ikinci mumun boylarının kaç saat sonra boylarının eşit olduğunu bulmak için iki mumunda doğrusal denklemlerini eşitleriz.
80-4x = 60-2x
80-60 = 4x-2x
2x=20
x=10 saat sonra boyları eşit olur.
- b) 1. mumun boyu 56 cm kaldığında 2. mumum boyu kaç cm olur?
1. mumun boyu 56 cm olması için kaç saat geçmesi gerektiğini bulmak için 1.mumun doğrusal denklemini 56 cm eşitleriz.
80-4x = 56
80-56 = 4x
24 = 4x
x = 6 saat sonra 1. mum 56 cm olur.
6 saat sonra 2. mumum boyunun kaç cm olacağını bulmak için ikinci mumun doğrusal denkleminde x yerine 6 yazmalıyız.
60-2x
60-2·6
60-12
48 cm ➡ 6 saat sonra ikinci mumun boyu






