Eşlik ve Benzerlik Konu Anlatımı

Eşlik ve Benzerlik Konu Anlatımı: Geometride eşlik ve benzerliğin temel ilkelerini, teoremlerini ve bu kavramların çeşitli geometrik problemlerdeki uygulamalarını anlayın.

ÜÇGENLERDE EŞLİK

İki üçgenin karşılıklı kenarının uzunlukları ve açılarının ölçüleri birbirine eşit ise bu üçgenler eş üçgenlerdir.

İki üçgenin eşliği “≅” sembolü ile gösterilir. Sembolle gösterirken eş olan açılar aynı sırada yazılmalıdır.

ÜÇGENLERDE EŞLİK ŞARTLARI

İki üçgenin karşılıklı tüm kenarlarının uzunlukları ve tüm açılarının ölçüleri eşitse bu iki üçgen eştir. Ancak iki üçgenin tüm kenarları ve tüm açıları her zaman verilmeyebilir. Böyle durumlarda bu kısıtlı verilere bakarak da biz iki üçgenin eş olup olmadığına kanaat getirebiliriz. Bunun için aşağıdaki eşlik şartlarını kullanırız. Eğer iki üçgen arasında bu şartlardan biri sağlanıyorsa bu iki üçgen eştir diyebiliriz.

1) Kenar – Kenar – Kenar Eşlik Şartı (KKK)

► İki üçgen arasında birebir eşleme yapıldığında karşılıklı tüm kenar uzunlukları eşit ise bu üçgenler eş üçgenlerdir. Buna;  Kenar – Kenar – Kenar (KKK) eşlik şartı denir.

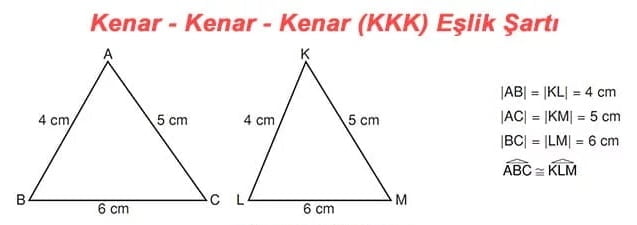
ÖRNEK: Aşağıdaki iki üçgen Kenar-Kenar-Kenar eşlik şartına göre eştir.

2) Kenar – Açı – Kenar Eşlik Şartı (KAK)

► İki üçgen arasında birebir eşleme yapıldığında ikişer kenar uzunlukları ve bu iki kenar arasında kalan açılarının ölçüleri eşit ise bu üçgenler eş üçgenlerdir. Buna;  Kenar – Açı – Kenar (KAK) eşlik şartı denir.

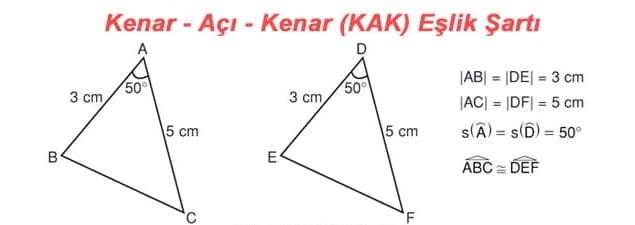
ÖRNEK: Aşağıdaki iki üçgen Kenar-Açı-Kenar eşlik şartına göre eştir.

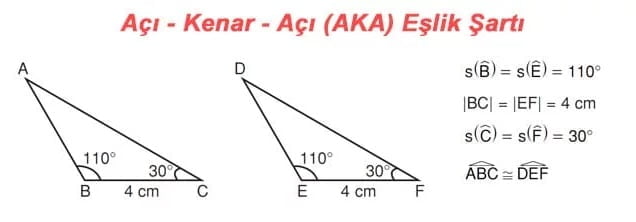
3) Açı – Kenar – Açı Eşlik Şartı (AKA)

► İki üçgen arasında birebir eşleme yapıldığında ikişer açılarının ölçüleri ve bu iki açı arasında kalan kenar uzunlukları eşit ise bu üçgenler eş üçgenlerdir. Buna;  Açı – Kenar – Açı (AKA) eşlik şartı denir.

ÖRNEK: Aşağıdaki iki üçgen Açı-Kenar-Açı eşlik şartına göre eştir.

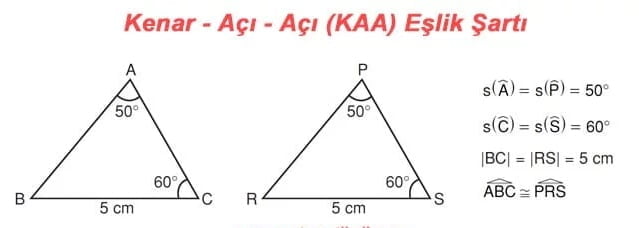
4) Kenar – Açı – Açı Eşlik Şartı (KAA)

► İki üçgen arasında birebir eşleme yapıldığında ikişer açılarının ölçüleri ve bu açılardan herhangi birinin karşısındaki kenarın uzunlukları eşit ise bu üçgenler eş üçgenlerdir. Buna;  Kenar – Açı – Açı (KAA) eşlik şartı denir.

ÖRNEK: Aşağıdaki iki üçgen Kenar-Açı-Açı eşlik şartına göre eştir.

ÜÇGENLERDE BENZERLİK

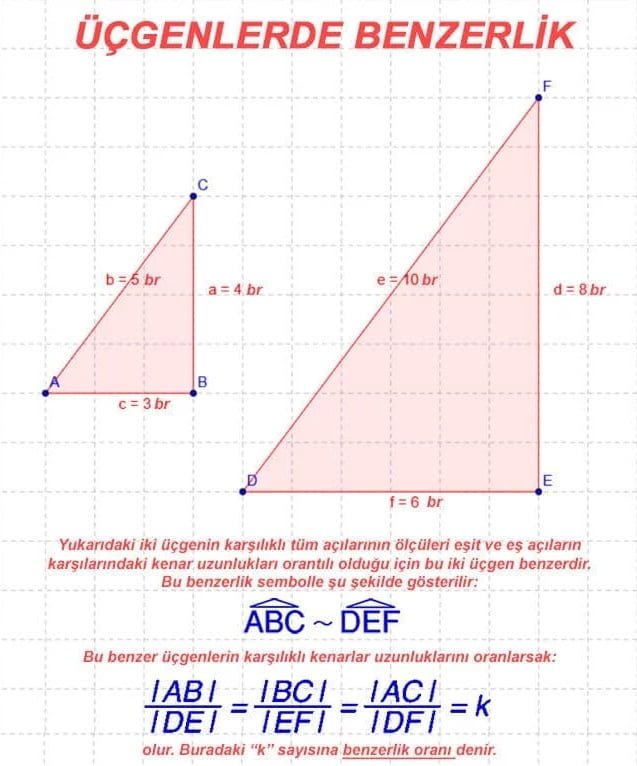
► İki üçgenin karşılıklı  açılarının ölçüleri birbirine eşit ve karşılıklı kenarlarının uzunlukları orantılı ise bu üçgenler benzer üçgenlerdir.

► İki üçgenin benzerliği “∼” sembolü ile gösterilir. Sembolle gösterirken eş olan açılar aynı sırada yazılmalıdır.

► Benzer iki üçgende karşılıklı kenarları oranlarsak bu oranlar bir sayıya eşit olur. Bu sayıya benzerlik oranı denir. Genelde k harfi ile gösterilir.

Örneğin aşağıdaki örnekte benzerlik oranı 1/2’dir. Pay ve paydaların yeri değişirse benzerlik oranı 2 olarak da yazılabilir.

Bu, “DEF üçgeninin kenar uzunlukları ABC üçgeninin 2 katıdır.” veya “ABC üçgeninin kenar uzunlukları DEF üçgeninin yarısıdır.” anlamına gelir.

ÜÇGENLERDE BENZERLİK ŞARTLARI

İki üçgenin tüm kenarları ve tüm açıları her zaman verilmeyebilir. Böyle durumlarda bu kısıtlı verilere bakarak da biz iki üçgenin benzer olup olmadığına kanaat getirebiliriz. Bunun için aşağıdaki benzerlik şartlarını kullanırız. Eğer iki üçgen arasında bu şartlardan biri sağlanıyorsa bu iki üçgen benzerdir diyebiliriz.

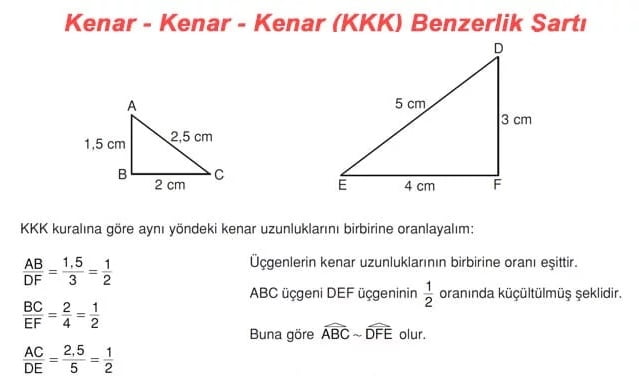
1) Kenar – Kenar – Kenar Benzerlik Şartı (KKK)

► İki üçgen arasında birebir eşleme yapıldığında karşılıklı kenar uzunluklarının oranı birbirine eşit ise bu üçgenler benzer üçgenlerdir. Buna;  Kenar – Kenar – Kenar (KKK) benzerlik şartı denir.

ÖRNEK: Aşağıdaki iki üçgen Kenar-Kenar-Kenar benzerlik şartına göre benzerdir.

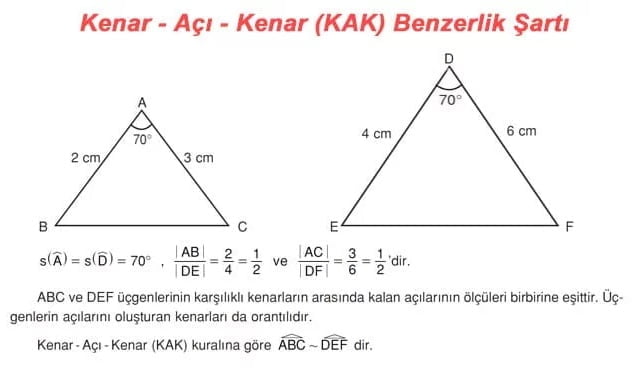
2) Kenar – Açı – Kenar Benzerlik Şartı (KAK)

► İki üçgen arasında birebir eşleme yapıldığında karşılıklı ikişer kenar uzunluklarının oranı ve bu iki kenar arasında kalan açılarının ölçüleri birbirine eşit ise bu üçgenler benzerdir üçgenlerdir. Buna;  Kenar – Açı – Kenar (KAK) benzerlik şartı denir.

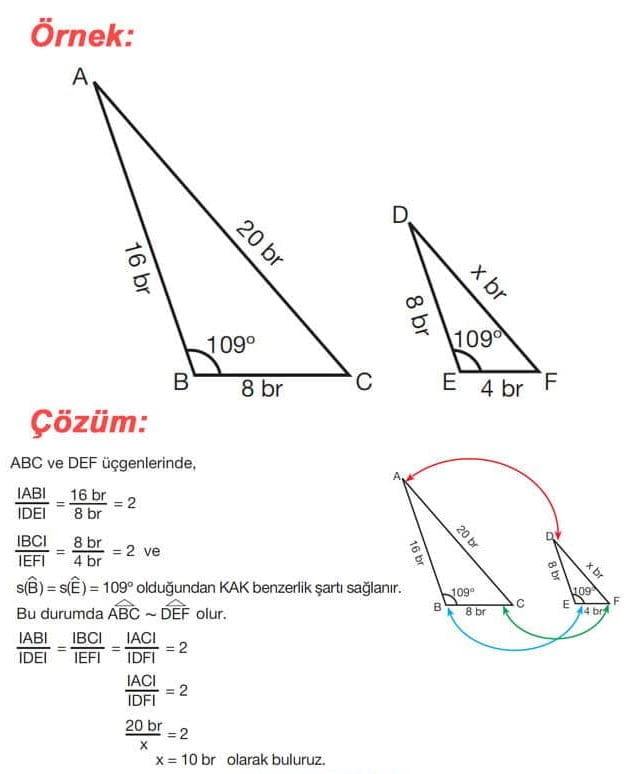
ÖRNEK: Aşağıdaki iki üçgen Kenar-Açı-Kenar benzerlik şartına göre benzerdir.

3) Açı – Açı Benzerlik Şartı (AA)

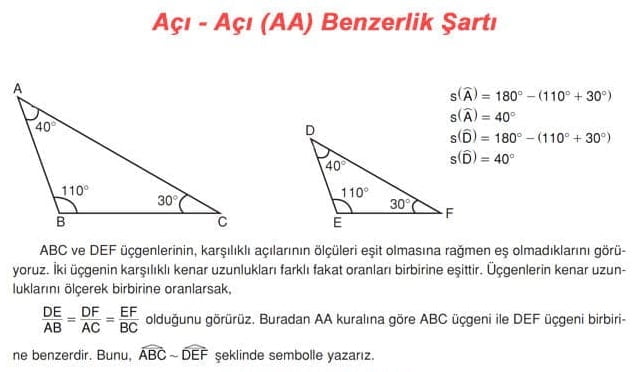
► İki üçgen arasında birebir eşleme yapıldığında karşılıklı iki açılarının ölçüleri birbirine eşit ise bu üçgenler benzer üçgenlerdir. Buna;  Açı – Açı (AA) benzerlik şartı denir. İki açıları eş olduğu için üçüncü açıları da eştir. Bu yüzden bu şarta Açı – Açı – Açı (AAA) benzerlik şartı da denilebilir.

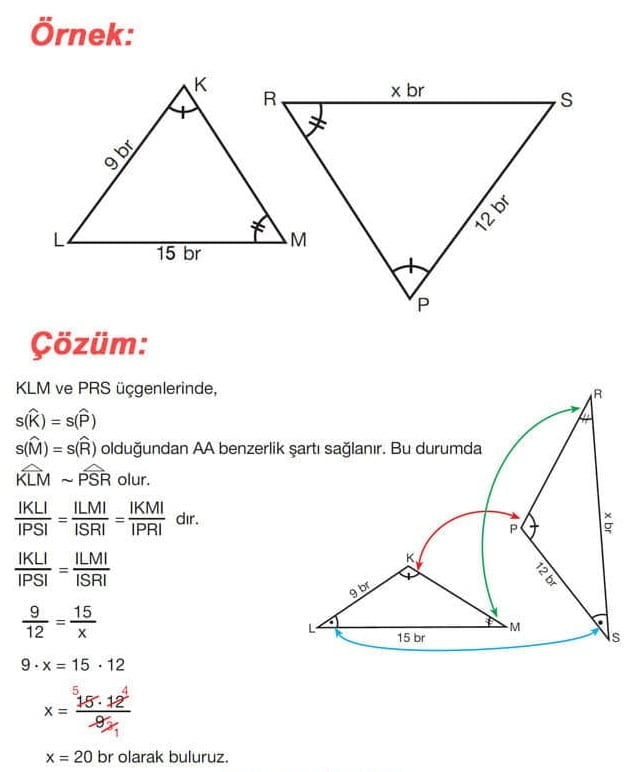
ÖRNEK: Aşağıdaki iki üçgen Açı-Açı benzerlik şartına göre benzerdir.

EŞLİK VE BENZERLİK İLE İLGİLİ

► Her eş üçgen aynı zamanda benzerdir, ancak her benzer üçgen eş olmak zorunda değildir.

► Eş üçgenler benzerlik oranı 1 olan benzer üçgenlerdir.

► İki üçgenin benzerlik oranı k ise çevreleri oranı da k’dır.

► İki üçgenin benzerlik oranı k ise karşılıklı yükseklikleri, açıortayları, kenarortayları oranı da k’dır.

► İki üçgenin benzerlik oranı k ise alanları oranı da k²‘dir.

ÖRNEKLER: Aşağıdaki üçgenlerde x ile gösterilen uzunlukları bulalım.