Dönüşüm Geometrisi Konu Anlatımı

Dönüşüm Geometrisi Konu Anlatımı: Geometrik şekillerin dönüşümünü anlayın; yansıma, döndürme ve öteleme gibi temel kavramları detaylıca öğrenin.

YANSIMA

KOORDİNAT SİSTEMİNDE YANSIMA (SİMETRİ)

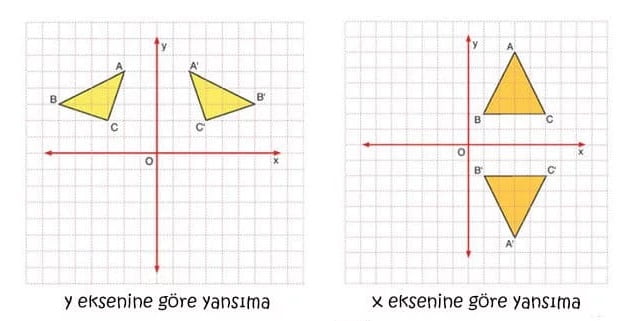
X Eksenine Göre Simetri

Bir şeklin X eksenine göre yansımasını çizmek için şeklin köşe noktalarının x eksenine dik uzaklığı bulunur, x ekseninin diğer tarafına x ekseninden bu kadar uzaklıkta noktalar belirlenir ve birleştirilir. Oluşan şeklin köşe noktalarının koordinatlarına bakılırsa şu görülecektir:

► “X” eksenine göre yansıma işleminde, yansıma sonrası apsisler (x değeri) değişmez iken ordinat değeri (y değeri) işaret değiştirir.

► A ( X , Y ) noktasının x eksenine göre yansıması olan noktanın koordinatları A’ ( X , – Y ) olur

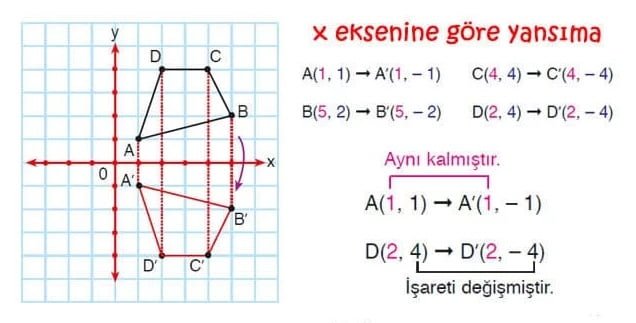
ÖRNEK: Aşağıda köşe noktalarının koordinatları A(1, 1), B(5, 2), C(4, 4) ve D(2, 4) olan ABCD dörtgeninin x eksenine göre yansıma altındaki görüntüsü (simetriği) verilmiştir. Dörtgenin köşelerinin koordinatlarının nasıl değiştiğini inceleyelim:

Y Eksenine Göre Simetri

Bir şeklin Y eksenine göre yansımasını çizmek için şeklin köşe noktalarının y eksenine dik uzaklığı bulunur, y ekseninin diğer tarafına y ekseninden bu kadar uzaklıkta noktalar belirlenir ve birleştirilir. Oluşan şeklin köşe noktalarının koordinatlarına bakılırsa şu görülecektir:

► “Y” eksenine göre yansıma işleminde, yansıma sonrası ordinatlar (y değeri) değişmez iken apsis değeri (x değeri) işaret değiştirir.

► A ( X , Y ) noktasının y eksenine göre yansıması olan noktanın koordinatları A’ ( – X , Y ) olur

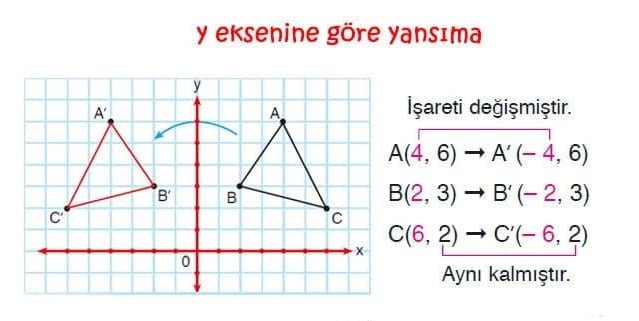
ÖRNEK: Aşağıda köşe noktalarının koordinatları A(4, 6), B(2, 3)ve  C(6, 2) olan ABC üçgeninin y eksenine göre yansıma altındaki görüntüsü (simetriği) verilmiştir. Dörtgenin köşelerinin koordinatlarının nasıl değiştiğini inceleyelim:

Orijine Göre Simetri

► Bir şeklin orijine göre simetriğini almak hem x hem de y eksenine göre simetriğini almakla aynı şeydir.

► A ( X , Y ) noktasının orijine göre yansımasının koordinatları A’ ( – X , – Y) olur

KOORDİNAT SİSTEMİNDE ÖTELEME

Bir şekli belirtilen doğrultuda ve birimde ötelemek için şeklin köşe noktaları o doğrultuda istenilen kadar kaydırılır ve birleştirilir.

X Eksenine Göre Öteleme

X ekseni boyunca öteleme yapılırken:

Sağa doğru öteleme yapılıyorsa öteleme miktarı noktanın apsisine (x değeri) eklenir.

► A ( X , Y ) noktası x eksenin göre Z birim sağa ötelenirse öteleme sonrası yeni koordinatları A’ ( X+Z , Y ) olur

Sola doğru öteleme yapılıyorsa öteleme miktarı noktanın apsisinden (x değeri) çıkartılır.

► A ( X , Y ) noktası x eksenin göre Z birim sola ötelenirse öteleme sonrası yeni koordinatları A’ ( X–Z , Y ) olur

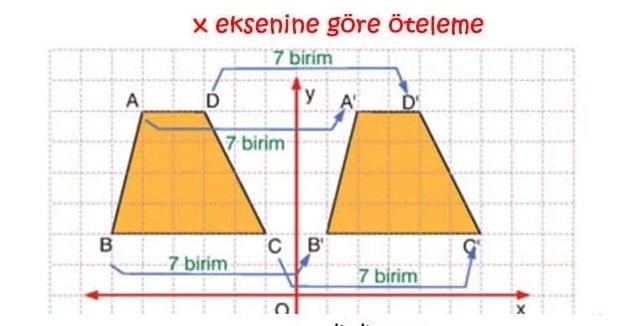
ÖRNEK: Aşağıdaki öteleme hareketini inceleyelim.

ABCD yamuğu 7 birim sağa ötelenmiştir. Bu yamuğun köşe noktalarının koordinatlarını incelersek:

A ( – 5 , 6 ) ► 7 br sağa ► A’ ( 2 , 6 )

B ( – 6 , 2 ) ► 7 br sağa ► B’ ( 1 , 2 )

C ( – 1 , 2 ) ► 7 br sağa ► C’ ( 6 , 2 )

D ( – 3 , 6 ) ► 7 br sağa ► D’ ( 4 , 6 )

Y Eksenine Göre Öteleme

Y ekseni boyunca öteleme yapılırken:

Yukarı doğru öteleme yapılıyorsa öteleme miktarı noktanın ordinatına (y değeri) eklenir.

► A ( X , Y ) noktası y eksenin göre Z birim yukarı ötelenirse öteleme sonrası yeni koordinatları A’ ( X , Y+Z ) olur

Aşağı doğru öteleme yapılıyorsa öteleme miktarı noktanın ordinatından (y değeri) çıkartılır.

► A ( X , Y ) noktası y eksenin göre Z birim aşağı ötelenirse öteleme sonrası yeni koordinatları A’ ( X , Y–Z ) olur

ÖRNEK: Aşağıdaki öteleme hareketini inceleyelim.

ABCD dikdörtgeni 5 birim aşağı ötelenmiştir. Bu dikdörtgenin köşe noktalarının koordinatlarını incelersek:

A ( – 5 , 2 ) ► 5 br aşağı ► A’ ( – 5 , – 3 )

B ( – 3 , 2 ) ► 5 br aşağı ► B’ ( – 3 , – 3 )

C ( – 3 , 5 ) ► 5 br aşağı ► C’ ( – 3 , 0 )

D ( – 5 , 5 ) ► 5 br aşağı ► D’ ( – 5 , 0 )

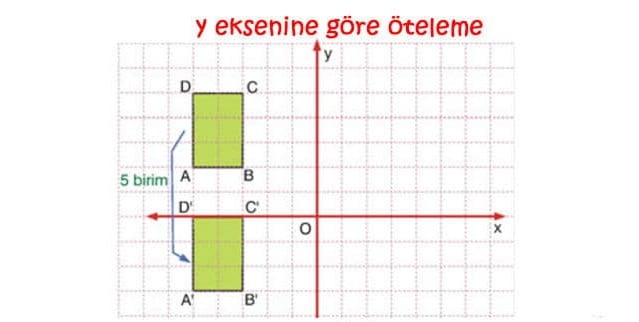
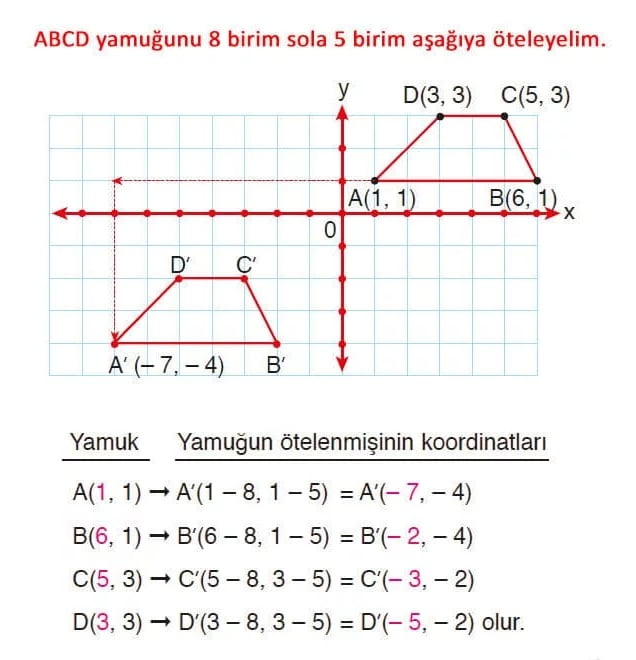
Öteleme ile ilgili şu soruyu inceleyelim.

KOORDİNAT SİSTEMİNDE ORİJİN ETRAFINDA DÖNME

Koordinat düzleminde verilen düzlemsel bir bölge (üçgen, dörtgen gibi) orijin etrafında, saatin dönme yönünde veya saatin dönme yönünün tersi yönünde döndürülebilir. Bu konuda bir şeklin saatin dönme yönünde veya tersi yönünde 90°, 180° , 270° ve 360° döndürülmesini göreceğiz.

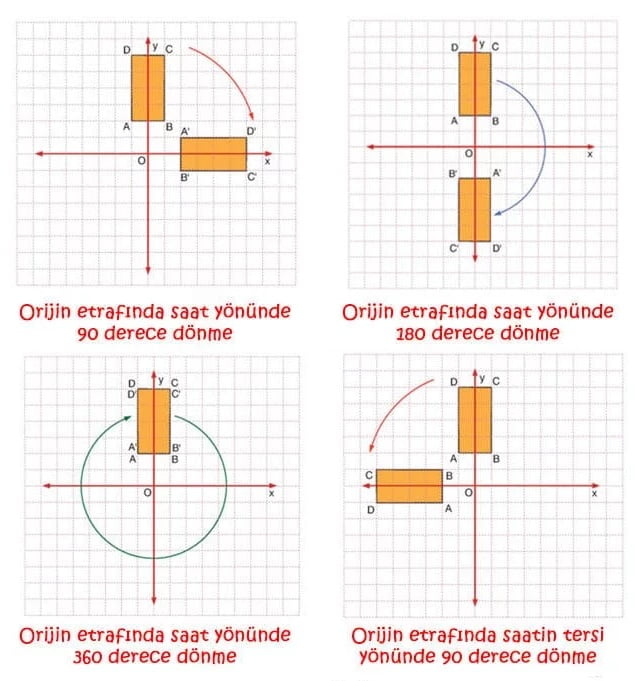
KURAL: Koordinat düzleminde A (x, y) noktasının orijin etrafında;

Saatin dönme yönünde 90° dönmesi sonucu koordinatları (y, – x),

Saatin dönme yönünde (veya tersi yönde) 180° dönmesi sonucu koordinatları ( – x, – y),

Saatin dönme yönünde 270° dönmesi sonucu koordinatları ( – y, x),

Saatin dönme yönünde (veya tersi yönde) 360° dönmesi sonucu koordinatları ( x, y ),

Saatin dönme yönünün tersi yönünde 90° dönmesi sonucu koordinatları (– y, x) olur.

NOTLAR:

► Bunların hepsini akılda tutmak yerine 90° dönme hareketi öğrenilip diğerlerinde bu işlemi üst üste tekrarlayabilirsiniz. Mesela 270° istiyorsa üç kere 90° döndürme yapabilirsiniz.

► Saatin tersi yönündeki bir dönme hareketi 360’tan çıkartılarak saat yönünde yapılabilir. Örneğin saatin tersi yönünde 90 derece döndürme, saat yönünde (360-90) 270 derece ile aynıdır.

► Bir şeklin orijin etrafında 180 derece dönmesi ile orijine göre simetriği aynıdır.

► Orjin etrafında dönme sonrasında elde edilen görüntü ile ilk görüntünün boyutları aynıdır.

► Bir şekildeki P noktasının orjine uzaklığı ile dönme işlemi sonucunda elde edilen görüntü üzerindeki P’ noktasının orjine uzaklığı aynıdır.

ÖRNEKLER

A (– 1, – 5) noktası saat yönünde 90° döndürülürse A'(– 5, 1) noktası elde edilir.

B (4, – 1) noktası saat yönünde 180° döndürülürse B’ (– 4, 1) noktası elde edilir.

C (– 2, 7) noktası saat yönünde 270° döndürülürse C’ (– 7, –2) noktası elde edilir.

D ( 3 , 5 ) noktası saat yönünde 360° döndürülürse D ( 3 , 5 )>noktası elde edilir.

ÖRNEK: Köşelerinin koordinatları A(7, -3), B(4, 7) ve C(-2, 5) olan ABC üçgeni saat yönünde 90° döndürülürse, yeni görüntüsünün koordinatlarını bulunuz.

A (7, – 3) noktası A’ (– 3, – 7)

B (4, 7) noktası B’ (7, – 4)

C (– 2, 5) noktası C’ (5, 2) olacaktır.