Geometrik Cisimler Konu Anlatımı

Geometrik Cisimler Konu Anlatımı: Üç boyutlu şekillerin dünyasını keşfedin, çeşitli geometrik cisimlerin özelliklerini ve hacim formüllerini öğrenin.
DİK PRİZMALAR
Alt ve üst tabanı birbirine eş ve paralel çokgensel bölge olan, yan yüzleri ise tabanlara dik dörtgensel bölge olan geometrik cisimlere dik prizma adı verilir.
Prizmalar tabanlarına göre isimlendirilir. Tabanları üçgen olan prizmaya üçgen prizma, tabanları dikdörtgen olan prizmaya dikdörtgenler prizması, tabanları altıgen olan prizmaya altıgen prizma adı verilir.
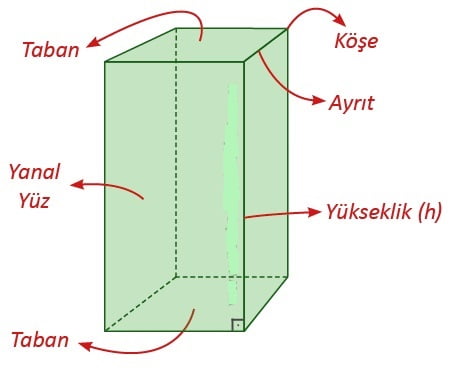
PRİZMANIN TEMEL ELEMANLARI
Prizmanın temel elemanları; taban, yanal yüz, ayrıt, köşe ve yüksekliktir.
► Dik prizmaların tabanları birbirine eş ve paraleldir.
► Dik prizmaların yanal yüzleri dikdörtgenlerden oluşur.
► Yüzeylerin kesiştikleri doğru parçaları prizmanın ayrıtlarıdır.
► Ayrıtların kesiştikleri noktalar prizmanın köşeleridir.
► Üst tabanın bir noktasından alt tabana indirilen dikmeye yükseklik denir ve “h” ile gösterilir.
► Dik prizmalarda yan ayrıtlar aynı zamanda yüksekliktir.
| Prizma | Taban Sayısı | Yanal Yüz Sayısı | Yüz Sayısı | Köşe Sayısı | Ayrıt Sayısı |
| Üçgen Dik Prizma | 2 | 3 | 5 | 6 | 9 |
| Dörtgen Dik Prizma | 2 | 4 | 6 | 8 | 12 |
| Beşgen Dik Prizma | 2 | 5 | 7 | 10 | 15 |
| Altıgen Dik Prizma | 2 | 6 | 8 | 12 | 18 |
| “n”gen Dik Prizma | 2 | n | n + 2 | 2.n | 3.n |
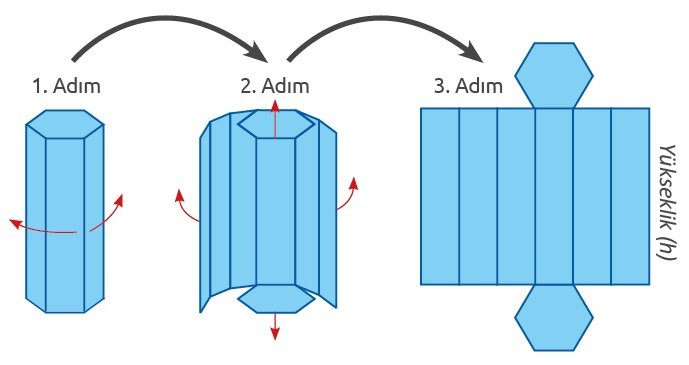
DİK PRİZMANIN AÇINIMI
Dik prizmaların açınımında; tabanları oluşturan 2 adet eş çokgen, yanal yüzleri oluşturan ve tabanın kenar sayısı kadar dikdörtgen yer alır.
Üçgen Dik Prizmanın Açınımı
Üçgen dik prizmanın açınımında 2 adet eş üçgen ve 3 adet dikdörtgen bulunur. Yanal yüzleri oluşturan dikdörtgenlerin birer kenarının uzunluğu prizmanın yüksekliğine eşittir. Bu dikdörtgenlerin diğer kenarlarının her birinin uzunluğu ise üçgenin bir kenar uzunluğuna eşittir.
Kare Dik Prizmanın Açınımı
Kare dik prizmanın açınımında 2 adet eş kare ve 4 adet eş dikdörtgen bulunur. Yanal yüzleri oluşturan eş dikdörtgenlerin bir kenar uzunluğu prizmanın yüksekliğine, diğer kenar uzunluğu karenin kenar uzunluğuna eşittir.
Dikdörtgen Dik Prizmanın Açınımı
Dikdörtgen dik prizmanın açınımında 6 adet dikdörtgen bulunur. Kapalı halde karşılıklı yüzlerde bulunan dikdörtgenler açınımda da birbirine eştir. Yanal yüzleri oluşturan dikdörtgenlerin bir kenar uzunluğu prizmanın yüksekliğine eşittir. Bu dikdörtgenlerin diğer kenarlarının her birinin uzunluğu ise tabanın bir kenar uzunluğuna eşittir.
Altıgen Dik Prizmanın Açınımı
Altıgen dik prizmanın açınımında 2 adet eş altıgen ve 6 adet dikdörtgen bulunur. Tabanlardaki altıgenler düzgün altıgen ise yanal yüzleri oluşturan dikdörtgenler birbirine eş olur. Dikdörtgenlerin bir kenar uzunluğu prizmanın yüksekliğine eşittir. Bu dikdörtgenlerin diğer kenarlarının her birinin uzunluğu ise tabanın bir kenar uzunluğuna eşittir.
DİK PİRAMİT
Bir çokgensel bölgenin tüm noktalarının bulunduğu yüzey dışındaki bir nokta ile birleşimine piramit denir. Yüksekliği tabanın merkezinden geçen piramide ise dik piramit denir.
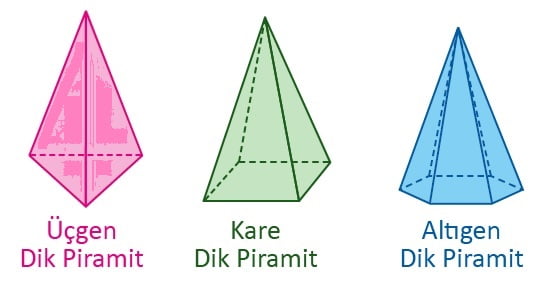
Piramitler tabanlarına göre isimlendirilir. Tabanı üçgen olan piramide üçgen piramit, tabanı dikdörtgen olan piramide dikdörtgen piramit, tabanı altıgen olan piramide altıgen piramit adı verilir.
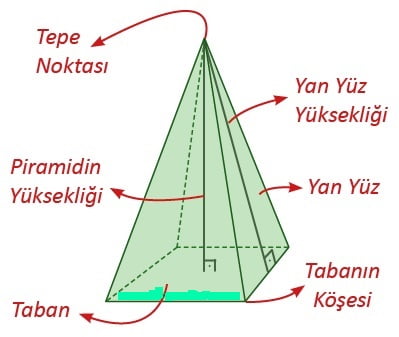
PİRAMİDİN TEMEL ELEMANLARI
Piramidin temel elemanları; taban, yanal yüz, ayrıt, tepe noktası ve yüksekliktir.
► Dik piramitlerin tabanı piramide ismini veren çokgensel bölgedir.
► Dik piramitlerin yanal yüzleri ikizkenar üçgenlerden oluşur.
► Yüzeylerin kesiştikleri doğru parçaları piramidin ayrıtlarıdır.
► Yanal ayrıtların kesiştikleri nokta tepe noktasıdır.
► Ayrıtların kesiştikleri noktalar piramidin köşeleridir.
► Tepe noktasından tabana indirilen dikmeye piramidin yüksekliği denir ve “h” ile gösterilir.
► Dik piramitlerde piramidin yüksekliği taban merkezine iner.
► Tepe noktasından tabana kenarlarına çizilen dikmelere yan yüz yüksekliği denir.
► Bir dik piramitte farklı yüzlerdeki yan yüz yüksekliklerinin uzunlukları birbirinden farklı olabilir.
| Piramit | Taban | Yanal Yüz Sayısı | Yüz Sayısı | Köşe Sayısı | Ayrıt Sayısı |
| Üçgen Dik Piramit | 1 | 3 | 4 | 4 | 6 |
| Dörtgen Dik Piramit | 1 | 4 | 5 | 5 | 8 |
| Beşgen Dik Piramit | 1 | 5 | 6 | 6 | 10 |
| Altıgen Dik Piramit | 1 | 6 | 7 | 7 | 12 |
| “n”gen Dik Piramit | 1 | n | n + 1 | n + 1 | 2.n |
DİK PİRAMİDİN AÇINIMI
Dik piramidin açınımında; tabanı oluşturan çokgen, yanal yüzleri oluşturan ve tabanın kenar sayısı kadar ikizkenar üçgen yer alır.
Yan yüz yükseklikleri dik piramidin açınımında gösterilebilir. Ancak piramidin yüksekliği açınımda yer almaz.
Üçgen Dik Piramidin Açınımı
Üçgen dik piramidin açınımında taban üçgeni ve yanal yüzleri oluşturan 3 adet ikizkenar üçgen bulunur.
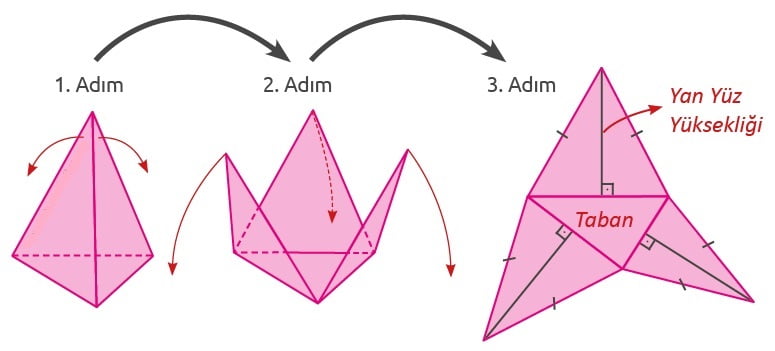
Kare Dik Piramidin Açınımı
Kare dik piramidin açınımında bir kare ve yanal yüzleri oluşturan 4 adet eş ikizkenar üçgen bulunur.
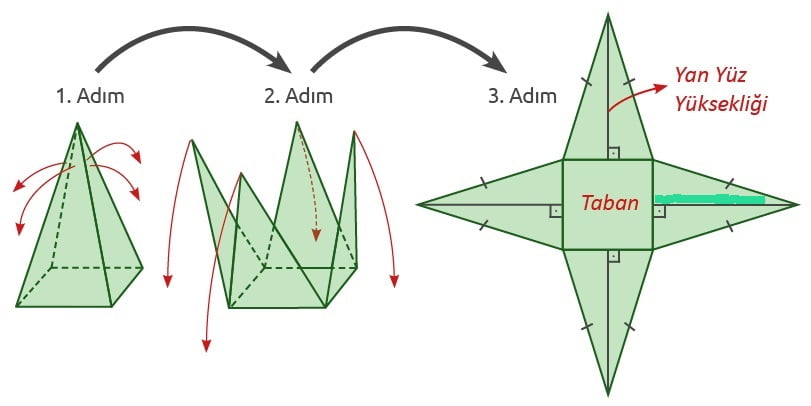
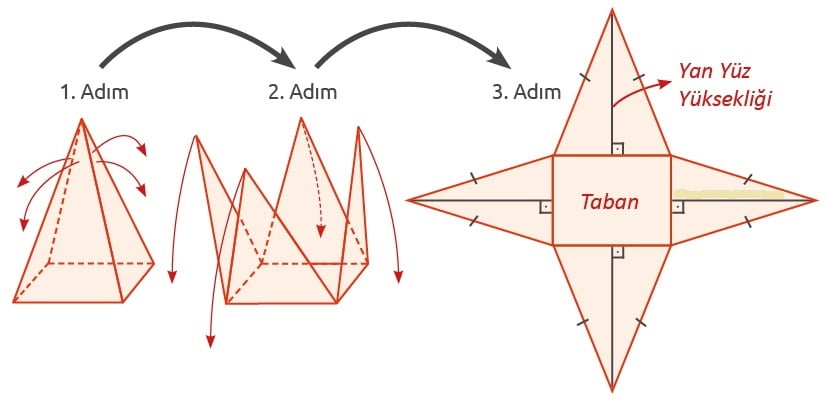
Dikdörtgen Dik Piramidin Açınımı
Dikdörtgen dik piramidin açınımında bir dikdörtgen ve yanal yüzleri oluşturan 4 adet ikizkenar üçgen bulunur. Bu üçgenler karşılıklı olarak birbirine eştir.
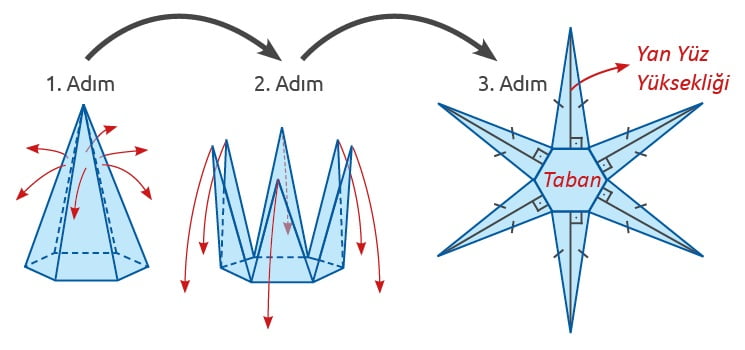
Altıgen Dik Piramidin Açınımı
Altıgen dik piramidin açınımında bir adet altıgen ve yanal yüzleri oluşturan 6 adet ikizkenar üçgen bulunur. Tabandaki altıgen düzgün altıgen ise yanal yüzleri oluşturan üçgenler birbirine eş olur.
DİK DAİRESEL KONİ
Bir dairenin bütün noktalarının daire düzlemi dışındaki bir nokta ile birleşimine koni denir. Yüksekliği tabanın merkezinden geçen koniye ise dik koni denir.
KONİNİN TEMEL ELEMANLARI
Koninin temel elemanları; taban, yanal yüzey, tepe noktası, ana doğrular, eksen, yarıçap ve yüksekliktir.
► Konide yer alan daireye taban denir.
► Tabanın yarıçapı koninin yarıçapıdır ve “r” ile gösterilir.
► Koniyi oluşturmak için taban dışında alınan noktaya tepe noktası denir.
► Tepe noktası ile taban merkezini birleştiren doğru parçasına eksen denir.
► Tepe noktasından tabana indirilen dikmeye yükseklik denir ve “h” ile gösterilir.
► Dik dairesel koninin ekseni tabana dik olduğu için eksen aynı zamanda yüksekliktir.
► Tepe noktası ile taban dairesinin çevresi üzerindeki bir noktayı birleştiren doğru parçalarına ana doğru denir ve “a” ile gösterilir.
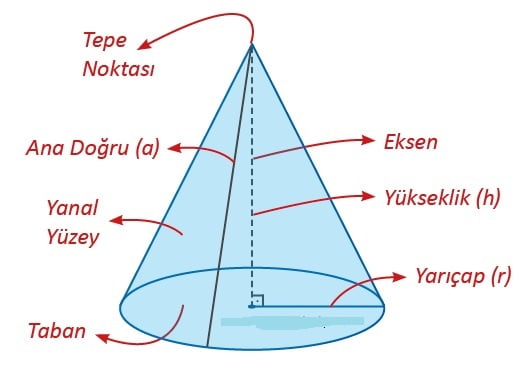
Koninin köşesi ve ayrıtı yoktur. Tabanı ve bir yanal yüzeyi vardır.
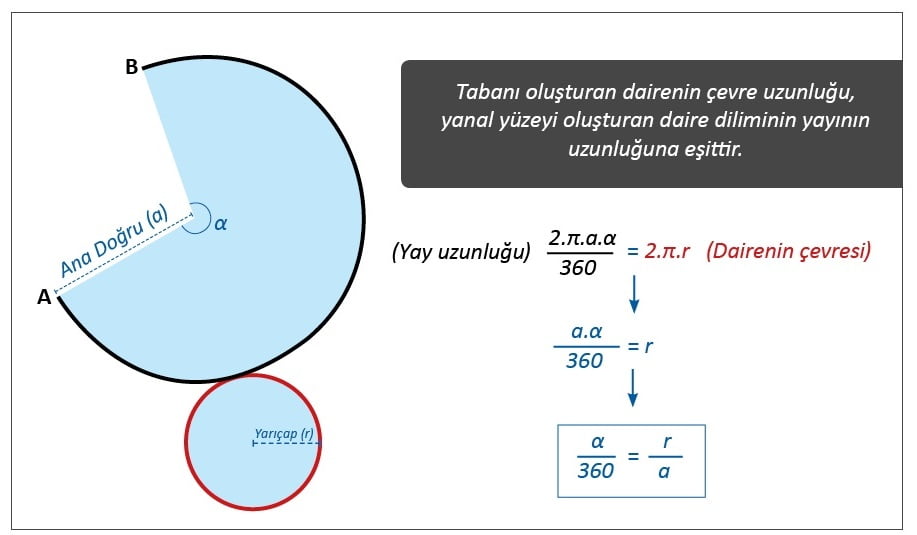
DİK KONİNİN AÇINIMI
Dik dairesel koninin açınımında; tabanı oluşturan daire, yanal yüzleri oluşturan daire dilimi yer alır.
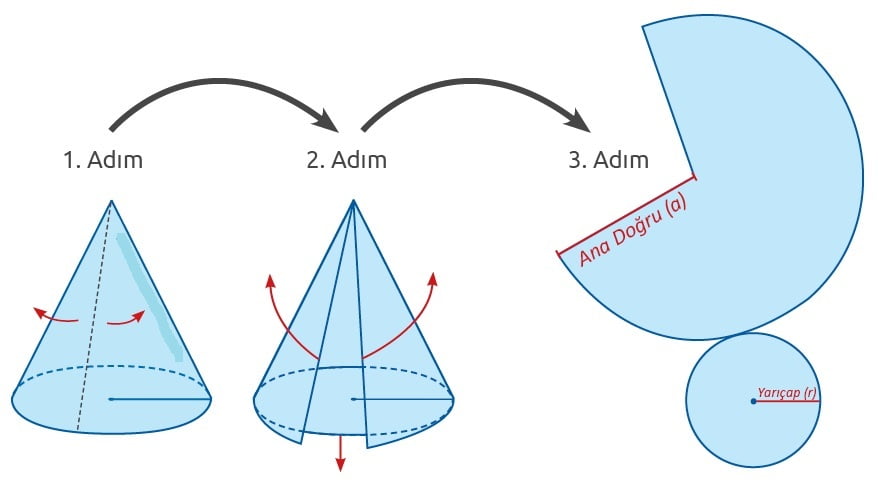
Dik dairesel konide yarıçap, yükseklik ve ana doğru dik üçgen oluşturur. Pisagor bağıntısından yararlanılarak aşağıdaki eşitlik elde edilir.
h2 + r2 = a2
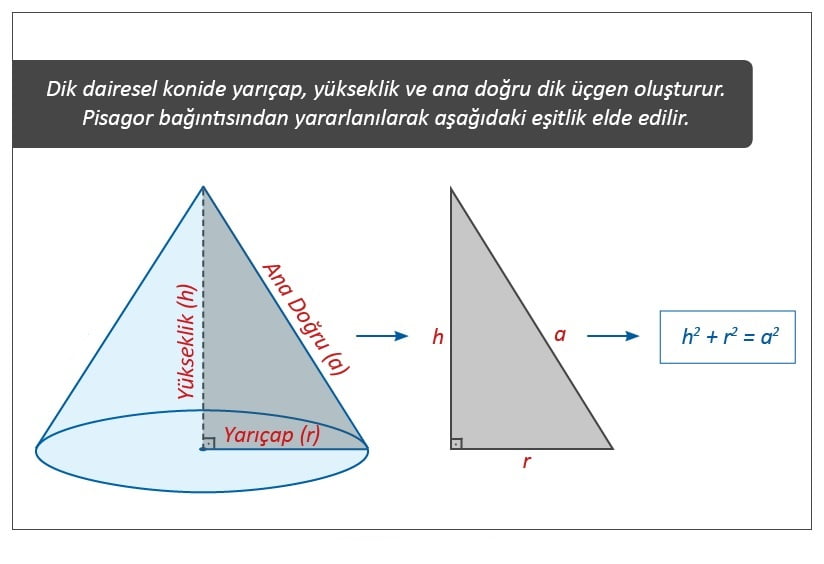
Konide tabanı oluşturan dairenin çevre uzunluğu, yanal yüzeyi oluşturan daire diliminin yayının uzunluğuna eşittir. Bu eşitlikten aşağıdaki eşitlik elde edilir.
TabandakiDaireninYarıçapı(r)/DaireDilimininYarıçapı(a) = DaireDilimininMerkezAçısı(α)/360
ÖRNEK: Taban yarıçapının uzunluğu 8 cm, yüksekliği 6 cm olan dik dairesel koninin açınımını çizelim.
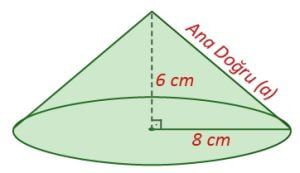
Önce ana doğrunun uzunluğunu hesaplayalım.
h2 + r2 = a2
62 + 82 = a2
100 = a2
a = 10 buluruz.
Şimdi açınımdaki daire diliminin merkez açısını hesaplayalım.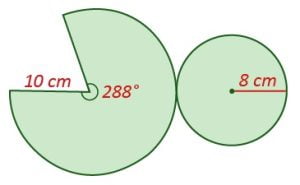
r/a = α/360
8/10 = α/360
10α=2880
α=288 buluruz ve bu ölçülere uygun çizim yaparız.
DİK DAİRESEL SİLİNDİR
Tabanları birbirine paralel eş dairelerden oluşan cisme silindir denir. Ekseni tabana dik olan silindire ise dik dairesel silindir denir.
SİLİNDİRİN TEMEL ELEMANLARI
Silindirin temel elemanları; tabanlar, yanal yüzey, ana doğrular, eksen, yarıçap ve yüksekliktir.
► Silindirde karşılıklı yer alan eş dairelere taban denir.
► Tabanların yarıçapları silindirin yarıçapıdır ve “r” ile gösterilir.
► Taban merkezlerini birleştiren doğru parçasına eksen denir.
► Üst tabanın bir noktasından alt tabana indirilen dikmeye yükseklik denir ve “h” ile gösterilir.
► Dik dairesel silindirin ekseni tabana dik olduğu için eksen aynı zamanda yüksekliktir.
► Tabanların karşılıklı iki noktasını bileştiren ve eksene paralel olan doğru parçalarına ana doğru denir.
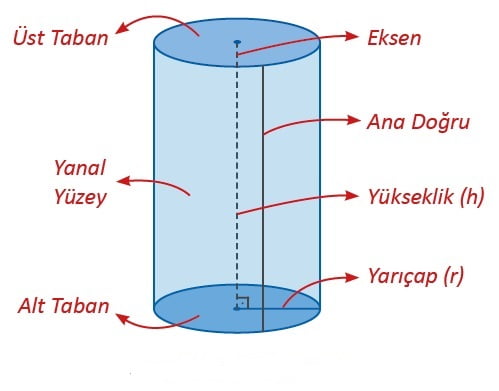
Silindirin köşesi ve ayrıtı yoktur. 2 tabanı ve bir yanal yüzeyi vardır.
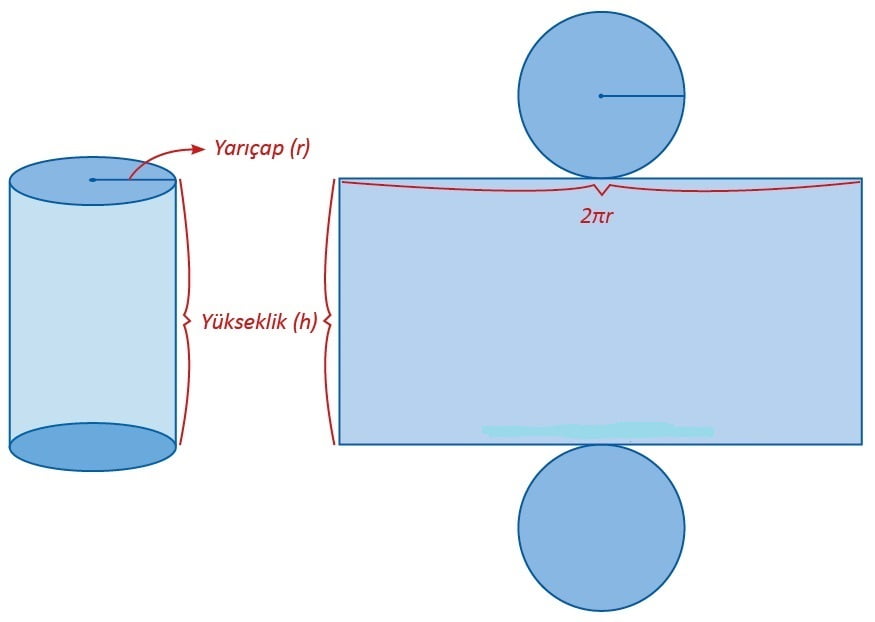
DİK DAİRESEL SİLİNDİRİN AÇINIMI
Silindirin açınımında; tabanları oluşturan 2 adet eş daire, yanal yüzeyi oluşturan 1 adet dikdörtgen yer alır.
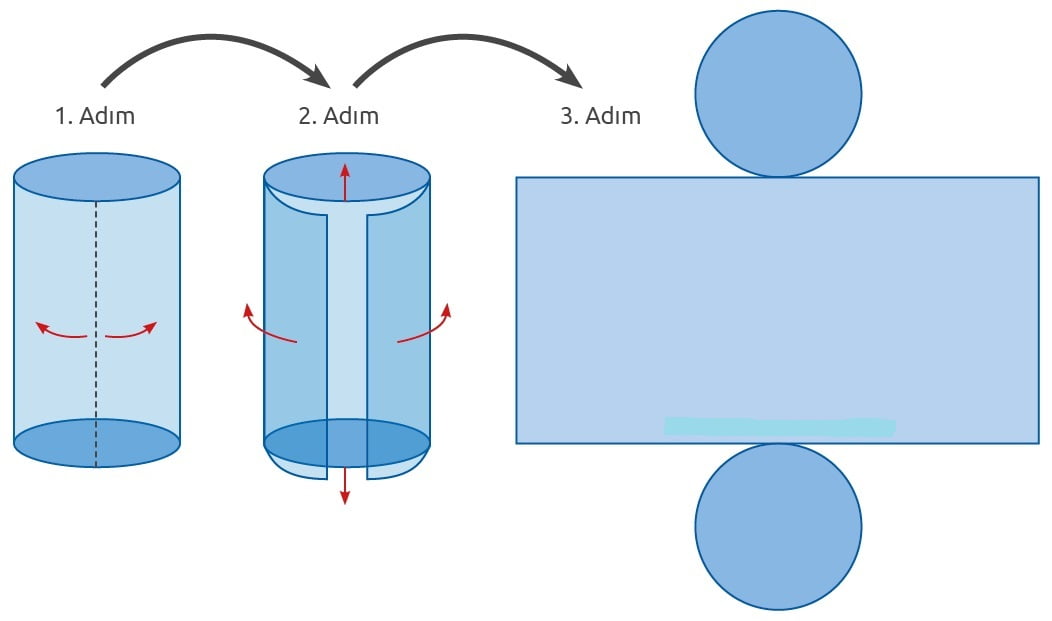
Silindirin yanal yüzeyini oluşturan dikdörtgenin bir kenarının uzunluğu silindirin yüksekliği uzunluğunda, diğer bir kenarı ise silindirin tabanının çevresi uzunluğundadır.
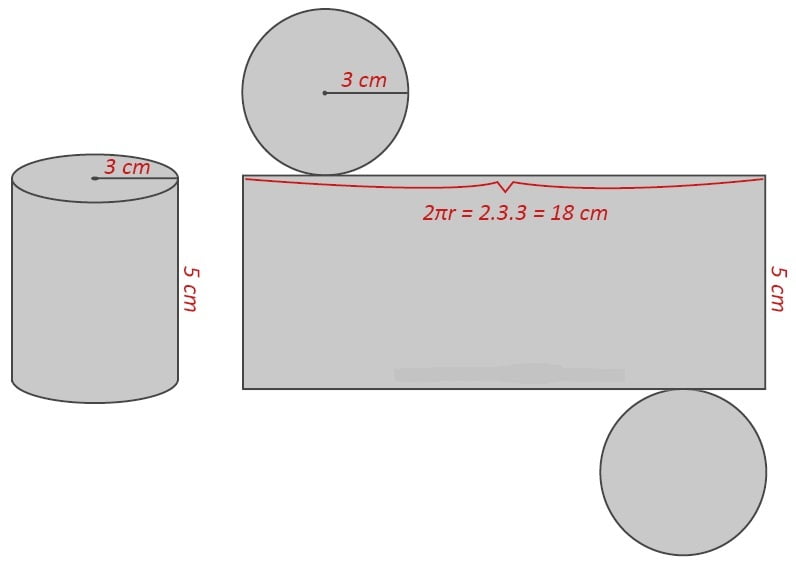
ÖRNEK: Aşağıda yüksekliği 5 cm, taban yarıçapı 3 cm olan bir dik dairesel silindirin açınımı verilmiştir. (Örnekte π = 3 olarak alınmıştır.)
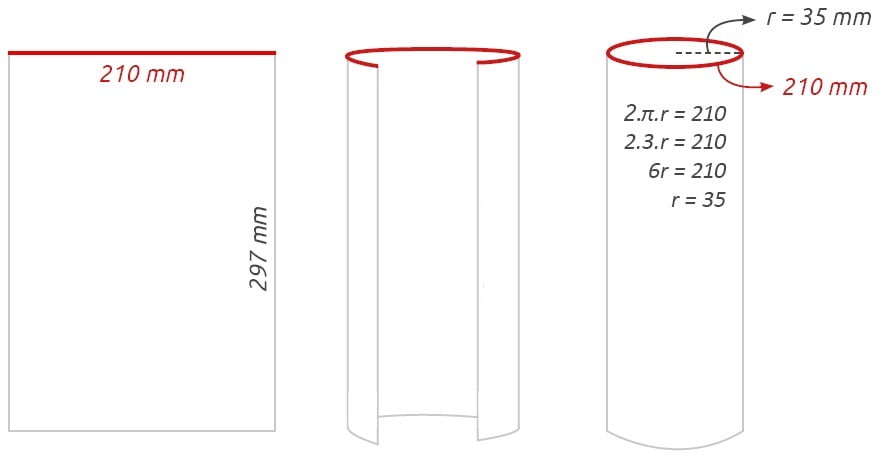
ÖRNEK: Bir A4 kağıdını (297 mm x 210 mm) uzun kenarları çakışacak şekilde rulo halinde katlanırsa taban yarıçapı kaç cm olur bulalım. ( π yerine 3 alınacaktır.)
A4 kağıdının uzun kenarları çakışacağı için silindirin yüksekliği 297 mm olacaktır. Kısa kenarı ise kıvrılıp tabandaki çemberin çevresine eşit olacaktır. Bu yüzden çemberin çevresini 210’a eşitleriz ve yarıçapını 35 mm olarak buluruz.
Silindirin Yüzey Alanı
Dik dairesel silindirin yüzey alanı, taban alanları ile yanal yüzeyin alanının toplamına eşittir.
Silindirin Yüzey Alanı = 2 . Taban Alanı + Yanal Yüzey Alanı
Silindirin açınımında 2 tane daire ve 1 tane dikdörtgen olduğunu biliyoruz. O zaman silindirin yüzey alanını bulurken bu bölgelerin alanlarını bulup toplarız.
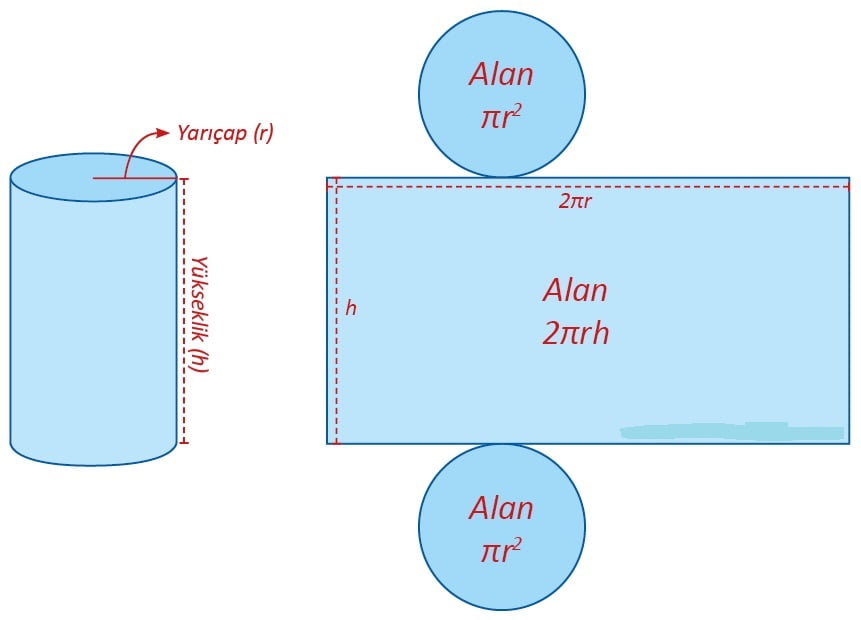
Silindirin Yüzey Alanı Formülü
Silindirin Taban Alanı = π r2
Silindirin Yanal Yüzey Alanı = 2 π r h
Silindirin Yüzey Alanı = ( 2 . Taban Alanı ) + ( Yanal Yüzey Alanı )
Silindirin Yüzey Alanı = 2 π r2 + 2 π r h
ÖRNEK: Yarıçapı 4 cm, yüksekliği 10 cm olan dik dairesel silindirin yüzey alanını bulalım. (π yerine 3 alınacak)
Silindirin Taban Alanı = 3.42 = 3.16 = 48 cm2
Silindirin Yanal Alanı = 2.3.4.10 = 240 cm2
Silindirin Yüzey Alanı = ( 2.Taban Alanı ) + ( Yanal Yüzey Alanı )
Silindirin Yüzey Alanı = ( 2.48 ) + ( 240 ) = 336 cm2
ÖRNEK: Çapı ve yüksekliği 10 cm olan dik dairesel silindirin yüzey alanını bulalım.
Soruda çapı 10 cm verildiği için yarıçap r = 5 cm olur. Ayrıca soruda π yerine kullanılacak bir değer verilmediği için formülde π olarak bırakacağız.
Silindirin Yüzey Alanı = 2 π r2 + 2 π r h
= 2.π.52 + 2.π.5.10
= 50π + 100π = 150π cm2
ÖRNEK: Yarıçapı 7 cm, yüksekliği 1 cm olan dik dairesel silindirin yüzey alanını bulalım. (π yerine 227 alınacak)
Silindirin Yüzey Alanı = 2 π r2 + 2 π r h
= 2.22/7.72 + 2.22/7.7.1 = 352 cm2
Silindirin Hacmi
Silindirin hacmi, taban alanı ile yüksekliğinin çarpımına eşittir.
Silindirin Hacmi = Taban Alanı . Yükseklik
Silindirin hacmi bulunurken aynı prizmalarda olduğu gibi taban alanı ile yükseklik uzunluğu çarpılır.
Silindirin Hacim Formülü
Dik dairesel silindirin tabanı daire şeklindedir. Bu yüzden hacim formülünde taban alanı yerine dairenin alanını veren ifade (πr2) yazılabilir.
Silindirin Hacmi = Taban Alanı . Yükseklik
Dik Dairesel Silindirin Hacmi = π r2 h
ÖRNEK: Yarıçapı 4 cm, yüksekliği 6 cm olan dik dairesel silindirin hacmini bulalım. (π yerine 3 alınacak)
Silindirin Hacmi = π r2 h = 3 . 42 . 6 = 288 cm3
ÖRNEK: Çapı ve yüksekliği 10 cm olan dik dairesel silindirin hacmini bulalım.
Soruda çapı 10 cm verildiği için yarıçap r = 5 cm olur. Ayrıca soruda π yerine kullanılacak bir değer verilmediği için formülde π olarak bırakacağız.
Silindirin Hacmi = π r2 h = π . 52 . 10 = 250π cm3
ÖRNEK: Yarıçapı 7 cm, yüksekliği 4 cm olan dik dairesel silindirin hacmini bulalım. (π yerine 227227 alınacak)
Silindirin Hacmi = π r2 h = 227227 . 72 . 4 = 616 cm3
ÖRNEK: Hacmi 1500 cm3 olan dik dairesel silindirin yüksekliği 5 cm ise yarıçapını bulalım. (π yerine 3 alınacak)
π r2 h = Silindirin Hacmi
3 . r2. 5 = 1500
15 r2 = 1500
r2 = 100
r = 10 cm






