Üslü İfadeler Konu Anlatımı

Üslü İfadeler Konu Anlatımı ile matematikteki üslü sayıların gücünü keşfedin; temel kavramları, kuralları ve problem çözme tekniklerini öğrenin.

ÜSLÜ İFADE NEDİR?

a ∈∈ R ve n ∈∈ Z⁺ olmak üzere aⁿ ifadesine üslü ifade denir. aⁿ ifadesinde a’ya taban, n’ye üs veya kuvvet adı verilir.

aⁿ = a.a.a…a (n tane)

ÖRNEK:

► 4³ = 4 . 4 . 4 = 64

► (−2)³ = (−2) . (−2) . (−2) = −8

► (1515)² = 1515 . 1515 = 125125

ÜSLÜ SAYILARIN ÖZELLİKLERİ

x, y ∈∈ R ve m, n ∈∈ Z⁺ olmak üzere

1. Kuvvet

Tüm gerçek sayıların birinci kuvveti kendisidir.

x¹ = x olur.

ÖRNEK:

► 7¹ = 7

► 0¹ = 0

► (−5)¹ = −5

► (1212)¹ = 1212

1. Kuvvet

Sıfır hariç her sayının 0. kuvveti 1’dir.

x ≠≠ 0 için x⁰ = 1 olur.

ÖRNEK:

► 5⁰ = 1

► (−7)⁰ = 1

► (5757)⁰ = 1

Negatif Kuvvet

Negatif kuvvette taban ters çevrilir.

ÖRNEK:

► 5⁻² = 152152 = 125125

► (−2)⁻⁶ = 1(−2)61(−2)6 = 164164

► (23)−3(23)−3 = (32)3(32)3 = 278278

Üslü Sayının Üssü

Üslü sayıların üssü alınırken üsler çarpılır.

(x^m)ⁿ = x^m.n

ÖRNEK:

► (2⁴)³ = 2^4.3 = 2¹²

► ((−8)⁻³)⁻² = (−8)^{(−3).(−2)} = (−8)⁶

Diğer Bazı Özellikler

• Pozitif gerçek sayıların tüm kuvvetleri pozitiftir.
• Negatif gerçek sayıların tek kuvvetleri negatif, çift kuvvetleri pozitiftir.
• 1’in tüm gerçek sayı kuvvetleri 1’dir.
• −1’in tek kuvvetleri −1, çift kuvvetleri +1’dir.
• 0’ın negatif kuvvetleri tanımsızdır.

ÜSLÜ SAYILARDA ÇARPMA VE BÖLME İŞLEMİ

Tabanları Aynı Olan Üslü İfadelerin Çarpımı

Tabanları aynı olan iki üslü sayının çarpımında üsler toplanır.

x^m . xⁿ = x^m+n

ÖRNEK:

► 5² . 5⁷ = 5²⁺⁷ = 5⁹

► (−4)⁻³ . (−4)⁵= (−4)⁻³⁺⁵ = (−4)²

Üsleri Aynı Olan Üslü İfadelerin Çarpımı

Üsleri aynı olan üslü sayıların çarpımında tabanlar çarpılır.

xⁿ . yⁿ = (x.y)ⁿ

ÖRNEK:

► 5⁹ . 2⁹ = (5.2)⁹ = 10⁹

► (−2)⁵ . (−3)⁵ . 8⁵= 48⁵

Tabanları Aynı Olan Üslü İfadelerin Bölümü

Tabanları aynı olan iki üslü sayının bölümünde bölünenin üssünden bölenin üssü çıkarılır.

x ≠≠ 0 için x^m : xⁿ = x^m−n olur.

ÖRNEK:

► 6¹² : 6¹⁷ = 6¹²⁻¹⁷ = 6⁻⁵

► 252−2252−2 = 2⁵⁻⁽⁻²⁾ = 2⁷

Üsleri Aynı Olan Üslü İfadelerin Bölümü

Üsleri aynı olan üslü sayıların bölümünde tabanlar bölünür.

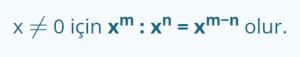
ÖRNEK:

► 15⁴⁵ : 3⁴⁵ = (153153)⁴⁵ = 5⁴⁵

► 7914979149 = (714)9(714)9 = (12)9(12)9

ÜSLÜ SAYILARDA TOPLAMA VE ÇIKARMA İŞLEMİ

Taban ve Üsleri Aynı Olan Üslü İfadelerle Toplama ve Çıkarma

Hem tabanları hem de üsleri aynı olan üslü sayılarda toplama ve çıkarma işlemi katsayılar arasında yapılır.

a . xⁿ + b . xⁿ − c . xⁿ = (a+b−c) . xⁿ

ÖRNEK:

► 5 . 2⁷ + 8 . 2⁷ = 2⁷ . (5 + 8) = 13 . 2⁷

► 4 . 9⁶ − 15 . 9⁶ = 9⁶ . ( 4 − 15) = −11 . 9⁶

Tabanları Aynı ve Üsleri Farklı Olan Üslü İfadelerle Toplama ve Çıkarma

Tabanları aynı, üsleri farklı olan üslü sayılarda toplama ve çıkarma işlemi yapılırken üsler eşitlenir ve daha sonra katsayılar arasında işlem yapılır.

ÖRNEK: 3¹⁴ + 3¹³ − 3¹² işleminin sonucunu bulalım.

Üsler, en düşük olan üsse göre eşitlenebilir. 3¹⁴ = 3² . 3¹² ve 3¹³ = 3 . 3¹² olduğu için bu sayılar yerine özdeşleri yazılır. Buna göre;

= 3¹⁴ + 3¹³ − 3¹²

= 3² . 3¹² + 3 . 3¹² − 3¹²

= 9 . 3¹² + 3 . 3¹² − 1 . 3¹²

= (9+3−1) . 3¹² = 11 . 3¹² olarak sonuç bulunur.

ÜSLÜ DENKLEMLER

İçinde üslü ifade bulunduran denklemlere üslü denklem adı verilir.

Eşitliğin her iki tarafındaki tabanlar −1, 0 ya da 1’den farklı ve üsler de 0’dan farklı gerçek sayı olmak şartıyla; tabanlar eşitse üsler de eşittir.

a ∈∈ R − {−1, 0, 1} ve x, y ∈∈ R − {0} olmak üzere a^x = a^y ise x = y dir.

ÖRNEK: Aşağıdaki denklemlerin çözümlerini bulalım.

►  3^x = 81

3^x = 3⁴ olduğu için x = 4

►  2^x+1 = 64

2^x+1 = 2⁶ olduğu için x = 5

►  5^x−3 = 25^2x

5^x−3 = (5²)^2x

5^x−3 = 5^4x

x−3 = 4x olduğu için x = −1

Eşitliğin her iki tarafındaki tabanlar −1, 0 ya da 1’den farklı gerçek sayı ve üsler de tam sayı olmak şartıyla; üsler eşit ve tek sayı ise tabanlar eşittir.

a, b ∈∈ R − {−1, 0, 1}, n ∈∈ Z − {0} ve n tek sayı olmak üzere aⁿ = bⁿ ise a = b dir.

ÖRNEK: Aşağıdaki denklemlerin çözümlerini bulalım.

►  64 = x³

4³ = x³ olduğu için x = 4

►  x⁷ = −128

x⁷ = (−2)⁷ olduğu için x = −2

►  (x+3)²¹ = 8⁷

(x+3)²¹ = (2³)⁷

(x+3)²¹ = 2²¹

x+3 = 2 olduğu için x = −1

Eşitliğin her iki tarafındaki tabanlar −1, 0 ya da 1’den farklı gerçek sayı ve üsler de 0’dan farklı tam sayı olmak şartıyla; üsler eşit ve çift sayı ise tabanların mutlak değeri eşittir.

a, b ∈∈ R − {−1, 0, 1}, n ∈∈ Z − {0} ve n çift sayı olmak üzere aⁿ = bⁿ ise | a | = | b | dir.

ÖRNEK: Aşağıdaki denklemlerin çözümlerini bulalım.

►  x⁴ = 16

x⁴ = 2⁴ olduğu için | x | = | 2 | olur.

| x | = 2 olduğu için de x = 2 ya da x = −2’dir.

►  (x+1)¹² = 8⁴

(x+1)¹² = (2³)⁴

(x+1)¹² = 2¹²

| x+1 | = | 2 | olduğu için x+1 = 2 ya da x+1 = −2’dir. Buradan da x = 1 ve x = −3 bulunur.

Bir üslü ifade 1’e eşit ise tabanı 1 olabilir, tabanı −1 ve üstü çift sayı olabilir ya da tabanı 0’dan farklı ve üssü 0 olabilir.
xⁿ = 1 eşitliği şu durumlarda sağlanır:
►  x ≠≠ 0 ve n = 0 tir.
►  x = 1 tir.
►  x = −1 ve n çift sayıdır.

ÖRNEK: (x−3)^{x + 1} = 1 denklemini sağlayan x değerlerini bulalım.

►  1. DURUM: Üs sıfır olabilir, üssü sıfır yapan değerin tabanı sıfır yapmaması gerekir.

x + 1 = 0 eşitliğinden x = −1 bulunur. Bu değer tabanı sıfır yapmayacağı için denklemi sağlar.

►  2. DURUM: Taban 1 olabilir.

x−3 = 1 eşitliğinden x = 4 bulunur.

►  3. DURUM: Taban −1 olabilir, tabanı −1 yapan değerin üssü çift sayı yapması gerekir.

x−3 = −1 eşitliğinden x = 2 bulunur. Bu değer üssü çift sayı yapmadığında denklemi sağlamaz.

x’in alabileceği değerler −1 ve 4’tür.